3. БУЛЕВЫ ФУНКЦИИ

Булевы операции, булева алгебра, булевы функции (то же, что и функции алгебры логики) начались систематически исследоваться в работах Дж. Буля (1815-1864) по символической логике.

§ 1. Основные булевы функции.

Булевой переменной называется переменная, имеющая только два возможных значения, которые будем обозначать через 0 и 1. Положим Е=0,1.

Функция f(x1,x2,…,xn) называется булевой(переключательной) функцией, если она может принимать только одно из двух возможных значений 0 или 1 в зависимости от значений своих аргументов x1,x2,…,xn, каждая из которых тоже принимает одно из значений 0 или 1. Таким образом, f(x1,x2,…,xn) булева функция тогда и только тогда, когда f функция из En в E.

Булеву функцию можно задать таблицей ее значений, которая и называется таблицей истинности.

Одной из основных булевых функций является функция отрицания, значение которой определяется по таблице:

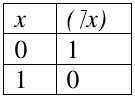
Отрицание является одноаргументной булевой функцией. Выражение «(¬ x)» читается «не x» и функцию отрицания можно интерпретировать как образование нового высказывания из высказывания x с помощью частицы «не». Введем следующие двухаргументные булевы функции по таблице:

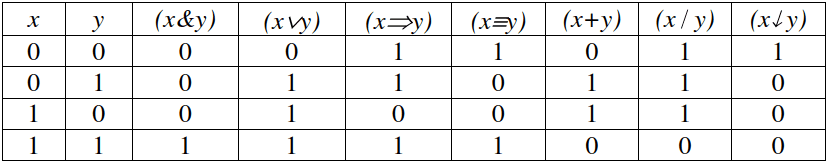
Функция (x&y) называется конъюнкцией x и y. Выражение «(x&y)» читается «x и y» и эту функцию можно интерпретировать как соединение двух высказываний x, y с помощью союза «и».

Функция (x∨y) называется дизъюнкцией x и y. Выражение «(x∨y)» читается «x или y» и эту функцию можно интерпретировать как соединение двух высказываний x, y связкой «или», где «или» понимается в соединительном (хотя бы одно), а не разделительном (либо-либо) смысле.

Функция (x⇒y) называется импликацией x и y. Выражение «(x⇒y)» читается «если x, то y» и эту функцию можно интерпретировать как образование из двух высказываний нового высказывания: «если x, то y». При этом x называется посылкой, а y заключением.

Функция (x ≡ y) называется эквивалентностью. Выражение «(x ≡ y)» можно читать «x эквивалентно y».

Функция (x+y)называется сложением по модулю два.

Функции $ (x| y) и (x↓ y)$ называются штрихом Шеффера и стрелкой Пирса соответственно.

Используя введенные функции, можно строить более сложные булевы функции с помощью операций суперпозиции функций, т. е. подстановки функций в функцию, например: $(¬ (x\&y)), ((x⇒y)\&(x≡ z)), ((x\&y)⇒(¬ z))$ и т. п. Значения полученных функций можно определять по таблицам истинности.

Таблица истинности функции от одного аргумента имеет две строки, от двух переменных – четыре, от трех переменных – восемь строк. В общем случае таблица истинности булевой функции от n переменных имеет ровно 2n строк, ибо добавление каждой новой переменной удваивает число строк.

Покажем, что число различных булевых функций от n переменных равно $N=2^{2^n}$ . Булева функция $f(x_1,x_2,...,x_n)$ принимает значения 0 либо 1 в зависимости от значений переменных$x_1,x_2,...,x_n$. Число различных наборов значений переменных$x_1,x_2,...,x_n$, как известно, равно $2^n$. На каждом из $2^n$ различных наборов функция $f(x_1,x_2,...,x_n)$ может принимать одно из двух значений. Следовательно, число различных булевых функций от n аргументов будет равно $N=2^{2^n}$ . С ростом n число N булевых функций от n аргументов резко растет. Например: для n=1 N=4; для n=2 N=16; для n=3 N=256; для n=5 N - более четырех миллиардов.

Переменная xk (1≤ k≤ n) функции $f(x_1,x_2,...,x_n)$ называется фиктивной или несущественной, если значение этой функции не меняются при изменении значений xk. Например, (x∨(x&y)) ~ x, следовательно, y является фиктивной переменной для функции f(x,y)=(x∨(x&y)).

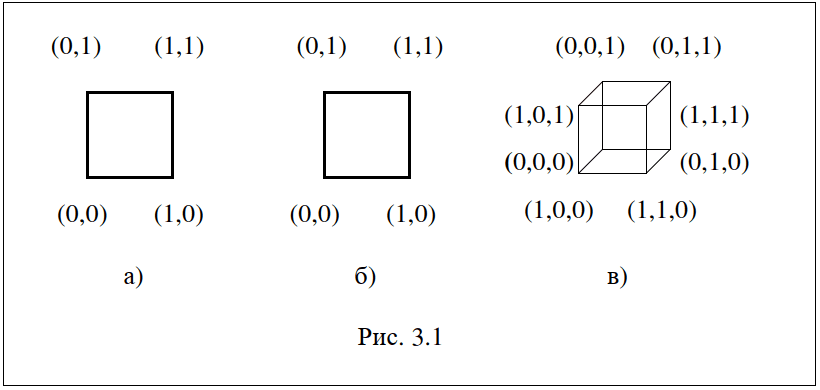
Булеву функцию можно задать с помощью таблицы, формулы (аналитически), графика и т.п. Графически булеву функцию $f(x_1,x_2,...,x_n)$ задают с помощью n-мерного куба следующим образом. Считаем наборы значений переменных $x_1,x_2,...,x_n$ вершинами n-мерного куба. Те вершины, на которых булева функция равна единице, помечаем точкой или звездочкой, остальные вершины оставляем без пометок. Например, функции (x⇒y), (x≡ y) и (x⇒(y&z)) можно представить их графиками, как на рис. 3.1 а, б и в соответственно.

Иногда булеву функцию называют переключательной функцией.