§ 16. Метод импликантных матриц

Метод импликантных матриц применяется для нахождения тупиковых и минимальных д.н.ф. Поясним этот метод на примере. Требуется найти минимальную д.н.ф. для функции

$f(x,y,z)=x\&y\&z∨x\&¬ y\&z∨¬ x\&¬ y\&z∨¬ x\&y\&¬ z∨¬ x\&¬ y\&¬ z∨x\&y\&¬ z$

Найдем для этой функции все простые импликанты, что равносильно отысканию сокращенной д.н.ф. Построим таблицу, вертикальными входами которой являются конституенты единицы исходной функции; во втором ее столбце будем записывать результаты, получающиеся при склеивании конституенты единицы; при этом звездочкой помечаем склеивающиеся конституенты.

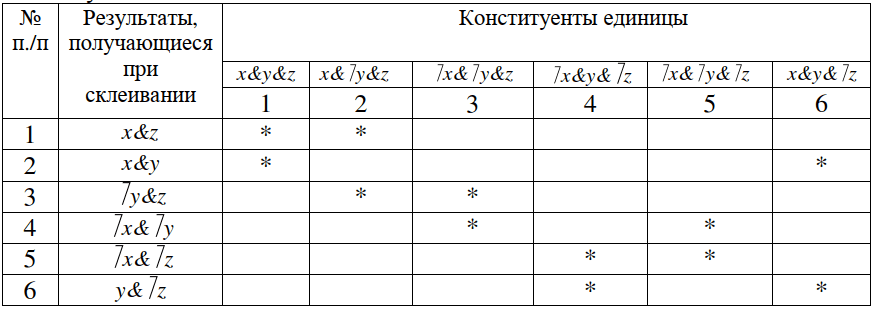
Если некоторое слагаемое не участвует в процедуре склеивания, то его переносим без изменения в столбец результатов рассматриваемой таблицы.

Для результатов, полученных в процессе операций склеивания (они записаны во втором столбце), строим аналогичную таблицу. Для этой таблицы вертикальными входами являются результаты склеивания, полученные в первой таблице. Далее осуществляем процедуру склеивания в новой таблице, затем строим следующую таблицу и так повторяем до тех пор, пока происходит склеивание. Если склеивание более невозможно, то результат, полученный во втором столбце последней таблицы, и даёт простые импликанты и, следовательно, сокращенную д.н.ф. Для рассматриваемого примера уже после первой таблицы не происходит склеивание, поэтому сокращенной д.н.ф. является:

$x\&z∨ x\&y ∨¬ y\&z∨¬ x\&¬ y∨¬ x\&¬ z∨y\&¬ z$

Слагаемые сокращенной д.н.ф. являются простыми импликантами.

Теперь строим импликантную матрицу. Построим таблицу, вертикальными входами которой являются конституенты единицы исходной функции, а горизонтальными входами - полученные простые импликанты.

Для каждой импликанты найдем конституенты единицы, собственной частью которых является данная импликанта. Например, импликанта x&z содержится в конституентах x&y&z и x&¬y&z (и поглощает эти конституенты), имликанта ¬ y&z содержится в конституентах x&¬ y&z и ¬ x& &¬ y&z и т.д. Клетки импликантной матрицы, образованные пересечением строк с импликантами и столбцов, с содержащими их конституентами, отметим каким-то символом, например, символом «*». Для того, чтобы получить минимальную д.н.ф. заданной функции, достаточно найти импликанты, которые совместно накрывают звездочками (*) все столбцы и в совокупности содержат наименьшее возможное число вхождений переменных (с отрицаниями или без отрицаний).

Для рассматриваемого примера первая построенная таблица является и импликантной матрицей. Из этой матрицы следует, что в минимальную д.н.ф. входят, например, x&z, ¬ x&¬ y и y&¬ z, ибо они в совокупности накрывают все столбцы символами «*». Форма x&y∨¬ x&¬ z∨¬ y&z тоже является минимальной д.н.ф. рассматриваемой функции. Обе эти д.н.ф., очевидно, являются и тупиковыми д.н.ф. рассматриваемой функции.

Если же взять импликанты x&z, ¬ x&¬ y, ¬ x&¬ z, x&y, то среди них не оказывается лишней, следовательно, получим новую тупиковую д.н.ф.: x&z∨¬ x&¬ y∨¬ x&¬ z∨x&y, которая не является минимальной д.н.ф. Можно построить и другие тупиковые д.н.ф. рассматриваемой функции.

Для уменьшения выкладок на этапе получения сокращенной д.н.ф. можно применить метод Мак-Класки. Этот метод является некоторой модификацией метода Квайна. В методе Квайна необходимо проводить попарное сравнение всех слагаемых с.д.н.ф. Число таких сравнений с ростом слагаемых быстро растет.

Идея Мак-Класки заключается в следующем. Если представить слагаемые с.д.н.ф. в виде их двоичных наборов, то эти наборы можно разбить по числу единиц в них на непересекающиеся группы. При этом в i-ую группу войдут все наборы, имеющие в своей записи точно i единиц. Попарное сравнение нужно производить только между элементами соседних по номеру групп. Так, вместо с.д.н.ф. вида

$x\&y\&¬ z ∨ x\&y\&z∨x\&¬ y\&¬ z∨¬ x\&¬ y\&¬ z$

можно рассмотреть наборы

(1 1 0), (1 1 1), (1 0 0), (0 0 0).

При склеивании слагаемых в разряды, соответствующие исключенным переменным, пишется знак тире. Такая модификация позволяет избежать громоздких записей.

Рассмотрим метод Мак-Класки на примере. Пусть f(x,y,z,t) равна единице на наборах, записанных в строках с номерами 0, 1, 2, 3, 4, 6, 7, 8, 9, 11 и 15. Найдем для этой функции сокращеннyю д.н.ф. и укажем, как найти минимальную и тупиковые д.н.ф.

Разобьем наборы значений переменных x, y, z, и t, на которых f(x,y,z,t)=1, на группы. В результате получим следующие группы:

нулевую: (0 0 0 0);
первую: (0 0 0 1), (0 0 1 0), (0 1 0 0), (1 0 0 0);
вторую: (0 0 1 1),(0 1 1 0), (1 0 0 1);
третью: (0 1 1 1), (1 0 1 1);
четвертую: (1 1 1 1).

В общем случае некоторые из групп могут оказаться пустыми. Сравнивая элементы соседних групп, получаем следующие группы:

нулевую: (0 0 0 -), (0 0 - 0), (0 – 0 0), (- 0 0 0);
первую: (0 0 - 1), (- 0 1 0), (0 0 1 -), (0 - 1 0), (0 1 - 0), (1 0 0 -);
вторую: (0 - 1 1),(- 0 0 1), (0 1 1 -), (1 0 - 1);
третью: (- 1 1 1), (1 - 1 1).

Приведем еще раз сравнение элементов соседних групп и получим группы:

нулевую: (0 0 - -), (0 - - 0), (- 0 0 -);
первую: (- 0 - 1), (0 - 1 -);
вторую: (- - 1 1).

Для полученных групп склеивание не происходит, поэтому получаем результат - сокращенную форму, которая имеет вид:

$¬ x\&¬ y∨¬ x\&¬ t∨¬ y\&¬ z∨¬ y\&t∨¬ x\&z∨z\&t$

Отметим, что если некоторые наборы не участвуют ни в каком склеивании, то они переходят без изменений на следующую итерацию.

Дальнейшее нахождение минимальных и тупиковых д.н.ф. совпадает с описанным ранее. Можно только упростить записи в импликантной матрице, записывая вместо переменной число (символ) 1, а вместо отрицания переменной – число (символ) 0.

Сокращенную д.н.ф. можно находить и другими способами, например, с помощью с.к.н.ф. Для этого выполняем следующие действия:

для заданной функции строим с.к.н.ф.;
в с.к.н.ф. раскрываем скобки, т.е. осуществляем преобразование типа &,∨ → ∨,&;
в полученном выражении удаляем противоречия, проводим поглощения: А∨А~А и А∨А&В~А.

В результате придем к сокращенной д.н.ф. Так, для примера, рассмотренного в начале данного параграфа, с.к.н.ф. имеет вид: $(x∨¬ y∨¬ z) \&(¬ x∨y∨z)$. Проведем указанные преобразования:

$(x∨¬ y∨¬ z)\&(¬ x∨y∨z)~ (x∨¬ y∨¬ z)\&(¬ x∨y∨z) ~ x\&¬ x∨x\&y∨x\&z∨¬ x\&¬ y∨y\&¬ y∨¬ y\&z∨¬ x\&¬ z∨y\&¬ z∨z\&¬ z ~ x\&y∨x\&z∨¬ x\&¬ y∨¬ y\&z∨¬ x\&¬ z∨ y\&¬ z$

Таким образом, сокращенная д.н.ф. найдена.