§ 13. Сокращенные дизъюнктивные нормальные формы

Прежде чем ввести сокращенные дизъюнктивные нормальные формы (сокращенные д.н.ф.), проведем вспомогательные рассуждения.

Импликантой булевой функции f называется булева функция ϕ, которая обращается в нуль на всех тех наборах значений аргументов, на которых равна нулю функция f. Обозначение ϕ ⊂ f применяется для высказывания: «функция ϕ является импликантой функции f», если ϕ не импликанта для f, то записываем: ϕ ⊄ f. Если ϕ ⊂ f, то всюду, где f принимает значение 0, функция ϕ тоже принимает значение 0, там же, где f принимает значение 1, ϕ может быть как 0, так и 1. Следовательно, функция ϕ имеет не меньшее количество значений 0, чем функция f.

Пример. Легко убедиться, что функция f(x,y)=x&y является импликантой для f(x,y)=x≡ y. Также легко видеть, что функция x⇒ y - импликанта для f(x,y,z)=(¬ y⇒¬ x)∨ z.

Функция ϕ(x,y)=x не является импликантой для f(x,y)=x&y, ибо f(1,0)=0, а ϕ(1,0)=1.

Очевидно, что функция, тождественно равная нулю (противоречие), является импликантой каждой булевой функции. Также очевидно, что каждая булева функция является импликантой функции, тождественно равной единице (тавтологии).

Собственной частью произведения называют произведение, полученное исключением из данного произведения одного или нескольких сомножителей.

Простыми импликантами булевой функции f называются такие элементарные произведения, которые сами являются импликантами функции f, но никакая собственная часть этих произведений не является импликантой этой функции. Например, если:

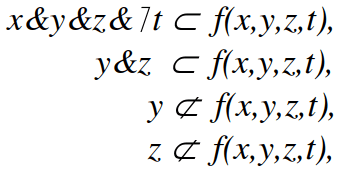
то y&z будет простой импликантой функции f(x,y,z,t).

Выясним, как найти импликанты и простые импликанты для заданной функции f(x1,x2,...,xn). Ясно, что можно рассмотреть все функции от переменных x1,x2,...,xn и среди них выделить импликанты и простые импликанты для функции f. Этот метод громоздкий и требует большого счета. Другой метод заключается в следующем.

Построим для f(x1,x2,...,xn) таблицы истинности. Если f тождественна равна нулю, то ее импликантой является только функция, тождественно равная нулю. Если f тождественно равна единице, то любая булева функция - импликанта для нее. Пусть f не тождественно равна нулю, тогда она обращается в единицу, например, в строках k1 ,k2 ,...,ks таблицы истинности. Для каждой из этих строк построим собственные конституенты единицы функции f. По построению каждая собственная конституента единицы Кi равна единице на наборе значений аргументов, записанных на ki-й строке, где f =1 и Кi = 0 на всех остальных наборах, в частности, и там, где f = 0.

Следовательно, каждая собственная конституента единицы функции f является импликантой для нее.

Далее для каждой из строк с номерами m1,m2,...,mr (r=2ⁿ - s), отличными от k1,k2,...,ks, построим по тем же правилам, что и ранее, конституенты единицы $К'j$ (1≤ j≤ r). Каждая такая конституента $К'j$ обращается в 1 на наборе, записанном в строке mj, а функция f при этом равна 0, следовательно, ни одно из $К'j$ не является импликантой для f.

Таким образом, только собственная конституента единицы Кi (1≤ i≤ r) функции f является импликантой для f, и эта собственная конституента сама

либо ее некоторая часть является простой импликантой для f. Отсюда следует, что каждая простая импликанта совпадает с одной из собственных конституент единицы функции f или является частью какой-либо из этих конституент. Поэтому, чтобы найти простые импликанты для f, можно рассматривать собственные конституенты единицы функции, всевозможные их части и среди них отыскивать простые импликанты. Данный способ тоже громоздкий. Существуют и другие методы, один из них (метод Квайна) рассмотрим в следующем параграфе.

Сокращенной д.н.ф. для булевой функции f(x1, x2, ..., xn) называется дизъюнкция всех простых импликант этой функции.

Из определения следует, что для каждой функции f сокращенная д.н.ф. единственна.

Теорема 3.17. Каждая булева функция f(x1, x2, ..., xn) равносильна своей сокращенной д.н.ф.

Доказательство. Пусть для f(x1, x2, ..., xn) построена ее сокращенная д.н.ф.:

$В_1∨ В_1∨...∨В_m$

где Вi - простые импликанты функции. Покажем, что на каждом наборе значений переменных x1, x2, ..., xn значения функции и суммы (3.22) совпадают.

Пусть на каком-то наборе значений переменных x1, x2, ..., xn функция f=0. Каждое Вi является импликантой для f, поэтому на выбранном наборе Вi =0 (1≤ i≤ m), следовательно, и вся сумма (3.22) обращается в нуль.

Далее, пусть $f(a_1, a_2, ..., a_n)=1$. Тогда на наборе $a_1, a_2, ..., a_n$равна 1 некоторая собственная конституента единицы функции f. Обозначим эту конституенту через К. Как уже показано, каждая конституента единицы функции f либо сама является простой импликантой, либо будет простой импликантой ее некоторая собственная часть. Следовательно, некоторое Вi из (3.22) совпадает с К, либо с её некоторой собственной частью. Если $a_1, a_2, ..., a_n$, то на наборе $В_i = К$ имеем$В_i(a_1, a_2, ..., a_n) = К(a_1, a_2, ..., a_n) =1$, если же Вi является собственной частью К, то, очевидно, Вi =1 на этом наборе. Тогда сумма (3.22) примет значение 1 на наборе $a_1, a_2, ..., a_n$. Теорема доказана.