§ 21. Функциональная декомпозиция

Пусть задана произвольная булева функция $f(x_1,x_2,...,x_n)$. Обозначим $Х=(x_1,x_2,...,x_n)$, тогда исходную функцию можно записать: f(Х).

Декомпозицией булевой функции f(Х) называется представление ее в виде

$f(Х)=g_0(Х^0,g_1(Х^1),...,g_k(Х^m))$

где k≥1, m≥1, Хi - некоторое подмножество множества переменных $Х,$ т.е. $Х^i = (x_{i_1}, x_{i_2},... x_{i_{k(i)}})$, $1≤ ij≤ n$, $1≤ j≤ k(i)$, $1≤ k(i)≤ n$, $1≤ i≤ m$, $g_l(Х^i)$, - некоторая булева функция, зависящая от множества переменных $X^i$, $ 1≤ l≤ k$, $ 1≤ i≤ m$.

Рассмотрим пример. Пусть $f(x,y,z)=x⇒ y\&z; Х={x,y,z} ; Х0= {x}, Х1 ={y,z}$. Тогда $f(x,y,z) = g_0(Х^0, g_1(Х^1)) =g_0(x, g1(y,z))$, где $g_0(x,y) = x⇒y, g_1(x,y)=x\&y.$

В зависимости от введенных выше чисел m и k, а также от способа разбиения множества Х на подмножества Хi различают несколько видов функциональной декомпозиции.

Если булева функция f(Х) допускает декомпозицию при k=1 и m=1, т.е. $f(Х)= g_0(Х^0, g_1(Х^1))$, то такая декомпозиция называется простой.

Число множеств Х i называется размерностью декомпозиции, а число k- кратностью декомпозиции. Размерность декомпозиции равна m+1.

Если декомпозиция выполняется при условии, что $Х^i∩Х^j =∅$ для любых i, j, i≠j, то декомпозиция называется разделительной. Если хотя бы одно пересечение подмножеств Хi и Хj не пусто, то декомпозиция называется неразделительной.

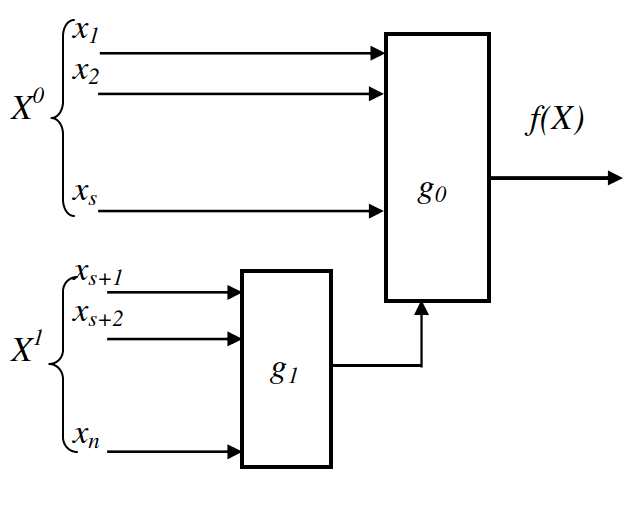
Подробно рассмотрим двумерную разделительную декомпозицию кратности один, которая является основой при исследовании других видов декомпозиции. Пусть $f(Х)= g_0(Х^0g_1(Х^1))$, $Х^0∩Х^1=∅$.

Структурная (функциональная) схема двумерной разделительной декомпозиции кратности один имеет вид, изображенный на рис.3.7. Для этой декомпозиции заданное множество аргументов разбивается на непересекающиеся множества $Х^0 = (x_1,x_2,...,x_s), Х1 =(x_{s+1},x_{s+2},...,x_n)$.

Ясно, что возможны и иные разбиения Х на Х0 и Х1. Для выяснения возможности декомпозиции строится декомпозиционная матрица, входами для столбцов которой являются всевозможные значения Х1, а входами для строк - всевозможные значения Х0. На пересечениях строк и столбцов записываются значения функции f.

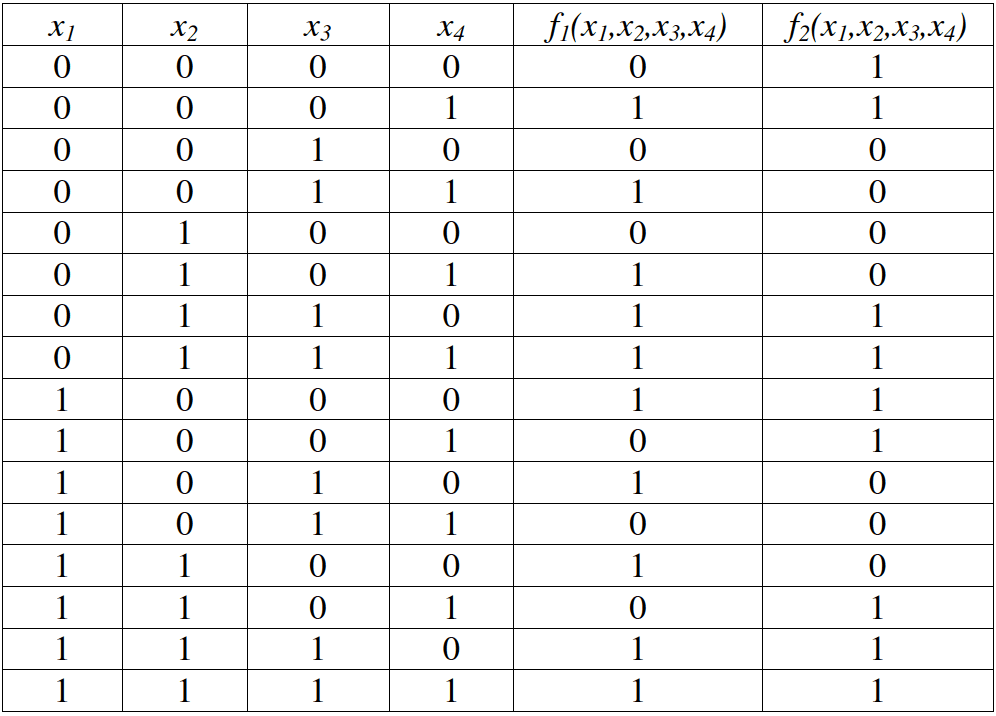
Рассмотрим пример построения декомпозиционной матрицы. Пусть имеем булеву функцию $f_1(x_1,x_2,x_3,x_4)=(x_1≡ x_4)⇒ x_2\&x_3$ и пусть $Х^0 = (x_1,x_4), Х^1 =(x_2,x_3)$ . Построим для этой функции сначала таблицу истинности.

Теперь построим декомпозиционную матрицу для $Х^0 = (x_1,x_4), Х^1 =(x_2,x_3)$ Эта матрица для функции $f_1(x_1,x_2,x_3,x_4)$ имеет вид:

Можно доказать следующую теорему.

Теорема 3.25. Булева функция f(Х), зависящая от n переменных, допускает двумерную разделительную декомпозицию кратности один тогда и только тогда, когда декомпозиционная матрица, соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х0 и Х1, содержит не более двух различных столбцов значений функций.

Из этой теоремы следует, что в рассмотренном примере функция f1 допускает требуемую декомпозицию, ибо декомпозиционная матрица имеет только два различных столбца значений функции f1 для заданных $X^0 = (x1,x4)$ и $X^1 = (x2,x3)$. Ясно, что имеем:

$f_1(x_1,x_2,x_3,x_4)=g_0(X^0,g_1(X^1))$

где

$g_0(X^0,s)=(x_1≡x_4)⇒ s, g_1(X^1)=x_2\&x_3$

Рассмотрим ещё функцию $ f_2(x_1,x_2,x_3,x_4)= x_1\&x_4⇒(x_2⇒ x_3) ⇒(x_2≡ x_3)$. Положим, что $Х^0 = (x_1,x_4) и Х^1 =(x_2,x_3).$. Значения этой функции приведены в записанной ранее таблице истинности. Тогда декомпозиционная матрица для $f_2(x_1,x_2,x_3,x_4)$ имеет следующий вид:

Построенная декомпозиционная матрица содержит три различных столбца значений функции f2 поэтому эта функция не допускает двумерную разделительную декомпозицию кратности один при заданных $Х^0 = (x_1,x_4)$ и $Х^1=(x_2,x_3)$.

Двумерной разделительной декомпозицией кратности k функции f является ее представление в виде:

$f(Х)=g_0(Х^0,g_1(Х^1), g_2(Х^1),...,g_k(Х^1 )). $

Структурная (функциональная) схема ее представлена на рис.3.8.

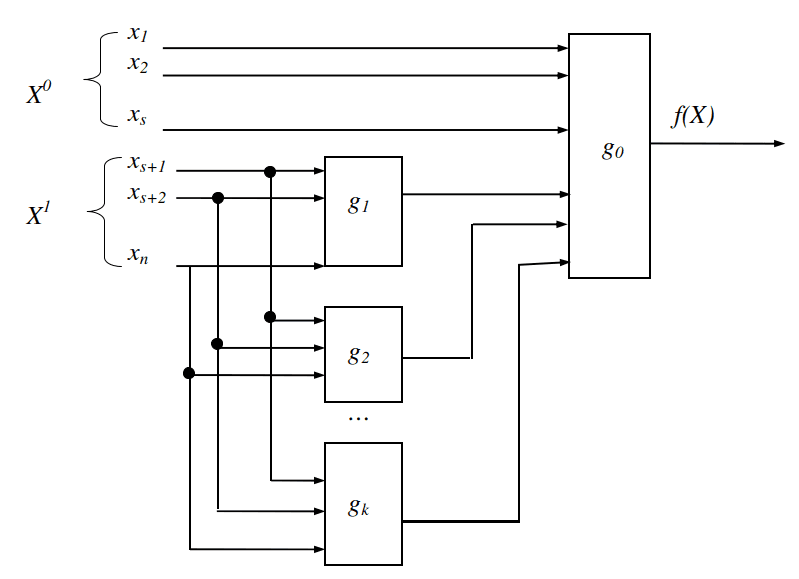
Можно доказать следующую теорему.

Теорема 3.26. Булева функция f(Х), зависящая от n переменных, допускает двумерную разделительную декомпозицию кратности k тогда и только тогда, когда декомпозиционная матрица функции f(Х), соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х0 и Х1, содержит не более чем 2k различных столбцов.

Для функции $f_2(x_1,x_2,x_3,x_4) = x_1\&x_4⇒(x_2⇒ x_3) ⇒(x_2≡ x_3)$ при $Х^0 = (x_1,x_4) и Х^1 =(x_2,x_3)$ её декомпозиционная матрица содержит три различных столбца значений этой функции, т.е. не более чем $2^2$ различных столбца. Следовательно, f2 допускает двумерную разделительную декомпозицию кратности 2 для заданных $Х^0 = (x_1,x_4) и Х^1 =(x_2,x_3)$. Ясно, что имеем:

$f_2(x_1,x_2,x_3,x_4)=g_0(X^0,g_1(X^1), g_2(X^1))$

где

$g_0(X^0, s, t)=(x_1\&x_4)⇒ s⇒ t, g_1(X^1)=x_2⇒ x_3, g_2(X^1)=x_2≡ x_3.$

В настоящее время получены критерии и для некоторых других видов как разделительной, так и неразделительной декомпозиций.