§ 19. Приложение теории булевых функций к анализу и синтезу контактных (переключательных) схем

Рассмотрим приложение теории булевых функций к анализу и синтезу контактных (переключательных) схем.

Контакты (переключатели) можно рассматривать как булевы переменные и обозначать буквами x, y, z,... или теми же буквами с числовыми индексами: x1, x2, ..., y1, y2 ,..., z1, z2,… Каждая из переменных может принимать одно и только одно из двух возможных значений: если контакт x разомкнут, то полагаем x=0, если контакт x замкнут, то x=1.

Под контактной (переключательной) схемой понимается схема, состоящая из замкнутых и разомкнутых контактов, соединенных параллельно или последовательно, или смешанным образом.

Отрицанием контакта x называется контакт, равный 1, если x=0, и равный 0, если x=1. Отрицание контакта x обозначается через ¬ x.

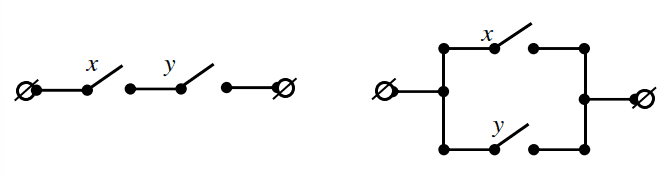
Очевидно, что последовательное соединение двух контактов x и y моделируется конъюнкцией переменных x и y, а параллельное соединение - их дизъюнкцией, см. рис. 3.2.

Известно, что любую булеву функцию можно представить, используя только ¬, &, ∨, причем ¬ относится только к буквам. Следовательно, любую булеву функцию можно представить в виде контактной схемы, в которой ток будет тогда и только тогда, когда функция принимает значение 1. Верно и обратное, каждую контактную схему можно представить в виде булевой функции таким образом, что эта функция принимает значение 1 тогда и только тогда, когда в схеме будет ток.

Используя булевы функции, можно строить контактные схемы, удовлетворяющие заданным требованиям (производить синтез контактных схем), а также преобразовывать, упрощать схемы (производить анализ контактных схем). Покажем это на примере.

Требуется построить контактную схему для голосования комитета из трех человек. При голосовании $"за"$ - нажатием кнопки свет должен загораться тогда и только тогда, когда $"за"$ проголосует большинство.

Решение. В нашем случае имеем три переменные. Обозначим их через x, y и z. По условию свет должен загораться тогда и только тогда, когда большинство этих переменных принимает значение 1, т.е. имеем таблицу:

Используя эту таблицу, находим булеву функцию, выбирая строки, оканчивающиеся на 1:

$¬ x\&y\&z∨ x\&¬ y\&z∨ x\&y\&¬ z∨ x\&y\&z$

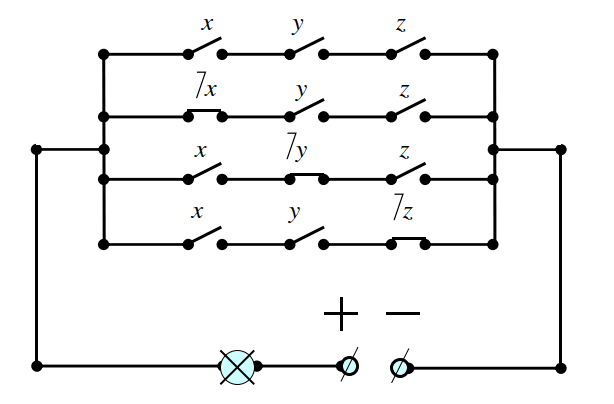
По этой функции строим схему, которая имеет четыре параллельные ветви, в каждой из которых по три контакта, см. рис. 3.3.

Эта схема выполняет поставленную задачу. Полученная схема содержит 12 контактов, и естественно попытаться проанализировать данную схему: нельзя ли, например, уменьшить количество контактов в переключательной схеме.

Можно получить, что для булевой функции (3.26) минимальная д.н.ф. равна: $x\&y∨x\&z∨y\&z$ , которую преобразуем к виду: $x\&y∨z\&(x∨y)$. Тогда схема будет содержать всего пять контактов см. рис. 3.4.

Очевидно, что анализ позволил сильно упростить контактную схему.