§ 11. Совершенные нормальные формы

Правая часть разложения (3.18) называется совершенной дизъюнктивной нормальной формой (с.д.н.ф.) для f, т.е. с.д.н.ф. это представление функции f в виде:

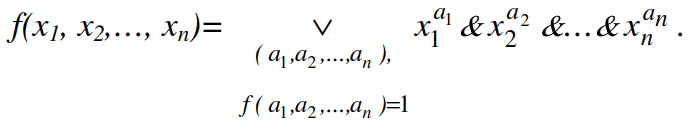
Очевидно, что с.д.н.ф. функции f(x1, x2,…, xn) это д.н.ф. этой функции, удовлетворяющая следующим условиям:

- нет одинаковых слагаемых;

- в каждое слагаемое входят все переменные x1,x2,…,xn один и только один раз (и только они) с отрицанием либо без отрицания.

С.д.н.ф. для функции f можно построить по таблице истинности этой функции. Для этого выбираем строки, где функция f равна 1; пусть это будут строки k1,k2,…,km. Для каждой выбранной строки ki, 1≤ i ≤ m, строим конституенту единицы Ki следующим образом. Если в выбранной строке ki переменная xj принимает значение 1, то в Ki она входит без отрицания, если же xj=0, то в Ki она входит с отрицанием. Дизъюнкция построенных конституент единицы и будет с.д.н.ф.

Конституенты единицы, построенные для строк, где функция f равна 1, называются собственными конституентами единицы функции f.

Рассмотрим пример на построение с.д.н.ф.

Пример. Пусть функция f(x,y,z) равна нулю тогда и только тогда, когда принимает значение нуль один и только один из аргументов функции. Найти с.д.н.ф. для f(x,y,z).

Решение. Составим таблицу истинности, исходя из задания функции.

Выберем строки, где f принимает значение 1, т.е. строки с номерами: 1,2,3,5 и 8. Для первой строки конституента единицы представляется в виде конъюнкции ¬x&¬y&¬z, для второй - ¬x&¬y& z. Построив таким образом собственные конституенты единицы данной функции, получим с.д.н.ф.:

$¬ x\&¬ y\&¬ z∨¬ x\&¬ y\& z∨¬ x\&y\&¬ z∨x\&¬ y\&¬ z∨x\&y\&z.$

Второй метод нахождения с.д.н.ф. – метод равносильных преобразований. Он применяется, когда булева функция задана в виде формулы и состоит в следующем. Для заданной формулы А находим д.н.ф. (которая всегда существует) и пусть д.н.ф. равна:

$D_1∨D_2∨…∨D_m (m ≥ 1),$

где Di (1≤ i≤m) – элементарное произведение. Построенная д.н.ф. может удовлетворять указанным условиям, тогда это с.д.н.ф.

Если в некоторое Di входит хотя бы одна переменная вместе с ее отрицанием, то Di – противоречие и из д.н.ф. Di можно исключить. Если при такой процедуре нужно отбросить все слагаемые из д.н.ф., то А – противоречие и с.д.н.ф. не существует.

Если в некоторое Di не входит одна из переменных xj формулы А, то заменяем Di на равносильную:

$(D_i\& x_j)∨( D_i\&¬x_j)$

Таким образом, добиваемся, чтобы каждое слагаемое содержало все аргументы формулы А.

Если в полученной форме окажутся одинаковые слагаемые, то оставляем только одно из них. В результате получим с.д.н.ф.

Правая часть разложения (3.20):

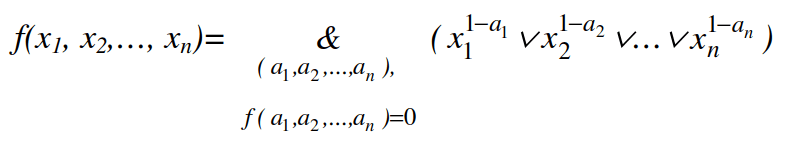
называется совершенной конъюнктивной нормальной формой (с.к.н.ф.) для f.

Очевидно, что совершенная к.н.ф. (с.к.н.ф.) определяются в терминах, двойственных к с.д.н.ф.

С.к.н.ф. функции f(x1,x2,…,xn), очевидно, является к.н.ф. этой функции, удовлетворяющая следующим условиям:

-нет одинаковых множителей;

-в каждый множитель входят все переменные x1,x2,…,xn один и только один раз (и только они) с отрицанием, либо без отрицания.

С.к.н.ф. для функции f можно построить по таблице истинности этой функции. Для этого выбираем строки, где f=0. Для каждой строки, где f=0, строим конституенту нуля K0 следующим образом. Если в выбранной строке переменная xj принимает значение 1, то в K0 она входит с отрицанием, если xj=0, то xj входит в K0 без отрицания. Конъюнкция построенных конституент нуля и будет с.к.н.ф.

Пример. Для функции f(x,y,z) предыдущего примера найдем с.к.н.ф. Нужно выбрать строки, где f=0. Это строки с номерами: 4, 6 и 7. В результате получим с.к.н.ф.:

$(x∨¬ y∨¬ z)\&(¬ x∨ y∨¬ z)\&(¬ x∨¬ y∨z). $

Второй метод построения с.к.н.ф. – метод равносильных преобразований, который применяется, когда булева функция задана в виде формулы и состоит в следующем: находим к.н.ф., затем добиваемся выполнения требуемых условий, вводя недостающие переменные согласно равносильности В∼(В∨x)&(В∨¬ x). При этом может оказаться, что исходная формула А тавтология и с.к.н.ф. не существует.