§ 17. Минимальные конъюнктивные нормальные формы

Как и для д.н.ф., для к.н.ф. можно ввести аналоги понятий импликанты, простой импликанты, сокращенной, тупиковой и минимальной к.н.ф. Для нас представляют интерес только минимальные к.н.ф. и методы их нахождения. Так как остальные указанные понятия играют при этом роль посредников, то постараемся по возможности их избежать или, по крайней мере, не описывать их.

Минимальной к.н.ф. булевой функции f называется к.н.ф., равносильная f, которая содержит наименьшее число вхождений переменных.

Как и минимальную д.н.ф., минимальную к.н.ф. находят в следующей последовательности.

Если функция f тождественно равна 1, то ее минимальной к.н.ф., очевидно, будет функция x∨¬ x.

Если функция f не тождественно равна 1, то сначала находят совершенную к.н.ф., по совершенной к.н.ф. - сокращенную к.н.ф., по сокращенной к.н.ф. - тупиковые к.н.ф. и из них выбирают минимальные к.н.ф. Мы не ввели определение сокращенной и тупиковой к.н.ф., не будем делать этого и далее, а только опишем процедуры (методы), позволяющие находить некоторые к.н.ф., которые можно считать сокращенными или тупиковыми по аналогии с дизъюнктивными формами.

Нахождение сокращенной к.н.ф. Считаем, что для заданной функции уже найдена совершенная к.н.ф. В этой с.к.н.ф. выполняют всевозможные операции неполного склеивания и затем операции поглощения. Операция неполного склеивания определяется следующим образом:

$(x∨ y)\&(x∨¬ y)~x\&(x∨y)\&(x∨¬ y)$

а операция поглощения - $x\&(x∨y)~x$

После выполнения этих операций будет получена сокращенная к.н.ф.

Метод имплицентных матриц для нахождения минимальной к.н.ф. состоит в следующем. Имплицентная матрица представляет собой таблицу, в верхнюю строку которой записываются конституенты нуля, содержащиеся в совершенной к.н.ф. этой функции, а в левый столбец - множители, содержащиеся в сокращенной к.н.ф. (которые называются простыми имплицентами). Клетки имплицентной матрицы, находящиеся на пересечении столбца с конституентой нуля, и строки с членом, который ее поглощает, отмечаются звездочками. Для построения минимальной к.н.ф. выбирают простые имплиценты, которые совместно накрывают звездочками (*) все столбцы и в совокупности содержат наименьшее возможное число вхождений переменных (с отрицаниями или без отрицаний).

Пусть требуется найти минимальную к.н.ф. для функции:

$(x∨y∨z) \& (¬ x∨y∨z)\&(x∨¬ y∨z)\&(x∨¬ y∨¬ z)$

Сокращенной к.н.ф., как легко видеть, будет $(y∨z)\&(x∨z)\&(x∨¬ y)$

Построим имплицентную матрицу:

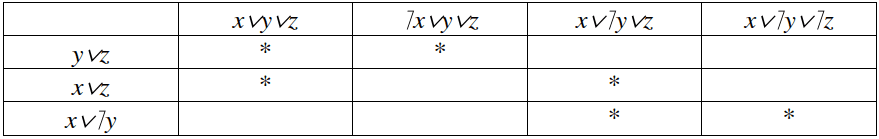
Видно, что имплиценты $y∨z $ и $x∨¬ y$ покрывают символами * все столбцы имплицентной матрицы, следовательно, $(y∨z)\&(x∨¬ y)$является минимальной к.н.ф.